O trabalho laboratorial realizado tinha como objectivo o estudo e análise do comportamento de dois sistemas mecânicos simples, o pêndulo simples e o pêndulo acoplado, ilustrativos dos fenómenos de oscilação que servem de base aos mais variados movimentos de índole oscilatória. Nomeadamente, estudar-se-ia primeiro o mais simples de todos estes movimentos, o movimento harmónico simples, recorrendo-se aos osciladores simples que os pêndulos constituem, analisando-se de seguida as características do movimento no caso de termos dois osciladores acoplados. Afirmemos também desde já que, apesar de ser possível estudar movimentos oscilatórios em duas ou três dimensões, vamos restringir-nos a apenas uma dimensão.

Principiemos, então, pelo estudo do oscilador harmónico simples. Antes de entrarmos em considerações específicas ao trabalho laboratorial e ao pêndulo simples utilizado como oscilador, vamos primeiro debruçarmo-nos um pouco sobre o movimento que pretendemos estudar. De forma básica, pode-se dizer que um dado corpo tem movimento harmónico simples quando a sua aceleração tem sentido contrário e é directamente proporcional ao seu deslocamento, isto é, o movimento é regido por uma equação diferencial de forma . O exemplo mais simples de um oscilador deste género, e que tipicamente é utilizado para o modelizar, é uma massa ligada a uma mola de constante , que tem o efeito de exercer sobre o corpo uma força resistente, , proporcional ao deslocamento do corpo. Aplicando a esta situação a conhecida segunda lei de Newton, (a força aplicada a um corpo é igual à variação da sua quantidade de movimento), vemos que:

Que é exactamente a equação apresentada atrás. A solução geral desta equação diferencial é , em que é a amplitude, é a frequência (angular) do movimento e é o ângulo de fase. Calculemos, agora que temos a expressão temporal do movimento harmónico simples, a sua velocidade e aceleração:

A primeira conclusão óbvia que podemos tirar é o facto de a expressão dada para o este movimento ser realmente solução da equação diferencial dada, já que:

Analisando com mais cuidado as expressões vemos que um corpo com movimento harmónico simples oscila a uma dada frequência angular em torno de um dado ponto central de equilíbrio, atingindo um deslocamento máximo de em relação a este (note-se que, sempre que se mencione o deslocamento do corpo, este será em relação ao ponto de equilíbrio). A sua velocidade tem um comportamento semelhante mas está desfasada de 90º em relação ao deslocamento, anulando-se quando este é máximo e atingindo o seu valor máximo, de , quando este é nulo, isto é, quando o corpo está na sua posição de equilíbrio. A sua aceleração é também harmónica, estando desfasada de 180º, isto é, está sempre em oposição ao deslocamento: quando mais o corpo se afasta do ponto de equilíbrio, maior a aceleração no sentido contrário. Se relembrarmos o exemplo simples de um oscilador harmónico dado anteriormente, um corpo preso por uma mola, facilmente nos apercebemos do quão lógicos são estes resultados. A mola terá um dado comprimento natural L e, no caso de não estar comprimida ou distendida, não exercerá qualquer força sobre o corpo, pelo que a aceleração sobre este será nula. O corpo encontra-se na sua posição de equilíbrio. Suponhamos agora que, por alguma razão, num dado instante o corpo não está na sua posição de equilíbrio e tem uma dada velocidade. Ora, a mola, agora comprimida ou distendida, vai exercer uma força sobre o corpo que tende a retorná-lo a sua posição de equilíbrio, força essa que, como já referimos, é proporcional ao deslocamento do corpo. Assim, quando o deslocamento é máximo também o é a aceleração (mas no sentido contrário), e, à medida que o corpo se aproxima do ponto de equilíbrio, esta vai diminuindo até se anular quando o deslocamento é nulo. Quanto à velocidade, vamos começar por supor que, no instante referido, o corpo está a afastar-se do ponto de equilíbrio. Ora, a aceleração do corpo é no sentido oposto da velocidade e esta diminui (de forma cada vez mais rápida, pois a valor da aceleração estava a aumentar) até que, num dado ponto, acaba por se anular: o ponto em que o deslocamento é máximo. Começa então novamente a aumentar, mas agora com o sentido da aceleração, isto é, no sentido de retornar o corpo à posição de equilíbrio. Ora, a partir do momento que corpo passe este ponto encontra-se na situação inicial em que se afasta dele e, novamente, a aceleração tem sentido contrário à velocidade. Esta será máxima, então, quando o deslocamento for zero. A respeito deste valor máximo da velocidade, , repare-se na sua proporcionalidade à frequência do movimento, o que está de acordo com o esperado se pensarmos no movimento de oscilação do corpo: de facto, para a mesma amplitude A do movimento, é lógico que, se o corpo completa mais oscilações num dado intervalo de tempo então a sua velocidade será também mais elevada.

Partindo do conhecimento do movimento harmónico simples é possível estudar, como já se referiu anteriormente, toda uma série de movimentos em que este esteja envolvido. Podíamos, por exemplo, analisar o que aconteceria caso fosse aplicada uma força externa ao sistema, como seria o movimento no caso de um oscilador não ideal (isto é, com amortecimento) ou, como faremos mais tarde, se tivéssemos dois osciladores acoplados. Como nos interessa, por agora, apenas o movimento de um oscilador harmónico simples, já que consideramos o amortecimento desprezável no trabalho laboratorial, não vamos estudar estes casos, limitando-nos a fazer uma breve referência ao caso de termos um oscilador simples, como apresentado anteriormente, mas agora com amortecimento não desprezável. De forma básica, representa-se o efeito do amortecimento por uma força de atrito , ficando então a equação diferencial que rege o movimento:

A solução desta equação, para valores da constante de decaimento menores que a frequência de oscilação no caso de não termos amortecimento, é dada por:

Em é a nova frequência angular de oscilação. As diferenças deste movimento para o anterior, em que se considerou um oscilador ideal, são a amplitude do movimento, que vai diminuindo (sendo amortecida...) exponencialmente com o tempo, eventualmente tornando-se nula, e a frequência de oscilação, que é menor.

Apesar de, como já referimos, ser possível modelizar o comportamento geral de um oscilador harmónico com o sistema massa-mola, vamos agora aproximar-nos um pouco mais do trabalho laboratorial em si ao estudarmos o caso do nosso sistema ser um pêndulo simples.

Tendo agora explicado de forma simples os princípios subjacentes ao oscilador harmónico simples que se pretendia estudar, vamos passar a uma análise do procedimento efectuado laboratorialmente e respectivos resultados. Comecemos, então, por uma breve referência à montagem efectuada e algumas das suas particularidades. Os dois pêndulos utilizados, que deste ponto em diante serão referidos como P1 (esquerdo) e P2 (direito), eram constituídos por uma barra rígida no fim da qual se encontrava uma massa. Foram medidos (ambos 84,7 cm) e colocados na barra de apoio a uma distância de 45 cm um de outro, tendo-se procurado estabelecer uma certa simetria na sua colocação em relação ao centro da barra. Assegurou-se também que estes se encontravam, na vertical, sobre pontos fixos e determinados na régua inferior, de modo a facilitar a medição dos deslocamentos horizontais dos pêndulos em relação à posição de equilíbrio. Note-se que esta precaução, apesar de aparentemente não ter grande relevância para o estudo do pêndulo simples, garantindo simplesmente uma maior simetria entre o procedimento efectuado em cada pêndulo, foi tomada sobretudo para o estudo dos osciladores acoplados e seus modos normais, que trataremos mais tarde, nos quais era indispensável garantir desvios para ambos os pêndulos o mais próximos possíveis. Por fim, tenha-se em conta um aspecto menor, o facto de a ligação do pêndulo esquerdo (P1) à barra de apoio ser ligeiramente diferente da do pêndulo direito (P2), possivelmente alterando um pouco os resultados em cada pêndulo.

O procedimento em si era simples, consistindo apenas na medição do período de oscilação de cada pêndulo. Para tal, ambos os pêndulos foram desviados um pouco (3 cm) da sua posição de equilíbrio e largados, medindo-se com um cronómetro o tempo necessário para que completassem vinte oscilações. Note-se que se mediu o tempo de vinte oscilações e não apenas de uma com o mesmo objectivo da repetição (ao longo de todo o trabalho) de todas as medições: minimizar os erros. De facto, podíamos, se nos limitássemos a apenas uma oscilação, cometer um erro por, por exemplo, inadvertidamente imprimir alguma velocidade inicial ao pêndulo, o que levaria a que este estivesse a partir não da posição de deslocamento máximo mas sim de algum ponto intermédio entre esta e o ponto de equilíbrio. Ao medirmos o tempo que o pêndulo levasse a voltar à posição de máximo deslocamento de onde supostamente o teríamos largado cometeríamos um erro pois o pêndulo ainda não teria completado uma oscilação completa desde o início da medição. O facto de medirmos o tempo necessário para que o pêndulo complete várias oscilações diminui, então, o efeito que um pequeno erro na medição do tempo da primeira oscilação possa ter no resultado final para o período do pêndulo, obtido dividindo o tempo medido pelo número de oscilações. Antes de se apresentar os resultados obtidos, note-se que, devido a dificuldades técnicas no que diz respeito aos cronómetros disponíveis, todos os tempos medidos estão afectados de um erro máximo de 0,025 segundos, não se podendo garantir uma maior precisão. As várias medições efectuadas nesta fase do trabalho laboratorial foram, então, as seguintes:

L = 84,7 cm à comprimento de ambos os pêndulos, medidos desde o ponto de apoio deste na barra até à base da massa.

Pêndulo esquerdo (P1)

Pêndulo direito (P2)

Os períodos de oscilação dos dois pêndulos, P1 e P2, eram de 1,72 e 1,73 segundos, respectivamente, podendo-se atribuir a pequena diferença entre eles (que teoricamente não deveria existir, já que ambos os pêndulos tinham o mesmo comprimento) a possíveis erros na medição do tempo que não foram suficientemente minimizados pela medição de um número elevado de oscilações, ou ao facto de os pêndulos não serem ideais, daí que pequenas diferenças entre eles pudessem afectar as medições, incluindo-se neste ponto a ligação dos pêndulos à barra de apoio, que não era exactamente igual. A diferença entre o período dos dois pêndulos, contudo, é bastante pequena e irrelevante face aos resultados que obteremos de seguida.

Vamos, para analisar os resultados obtidos, relembrar que, no caso do pêndulo simples, se verifica a relação , em que é a frequência angular do movimento, g é a aceleração da gravidade e L é o comprimento do pêndulo. Temos, então, que:

Ora, se considerarmos o valor de g de 9,8 ms^-2, temos que:

Um valor para o período de oscilação do pêndulo claramente superior aos obtidos. Vejamos agora, para os valores obtidos, quais seriam os valores da aceleração da gravidade e do comprimento do pêndulo correspondentes:

P1:

P2:

Estes resultados mostram o motivo de termos considerado a diferença entre o período dos dois pêndulos como irrelevante. De facto, as diferenças entre os resultados apresentados para ambos os pêndulos são insignificantes face à sua disparidade com os valores esperados teoricamente. Os erros relativos são de cerca de 15% no caso da aceleração da gravidade e de 13% no caso do comprimento do pêndulos. Não podemos, claramente, simplesmente desprezá-los, devendo procurar a razão de tão grandes diferenças. Como poderemos, então, explicar erros de tal magnitude? Poderíamos pensar que o erro estava nas medições efectuadas, mas tal hipótese parece absurda dada a magnitude do erros. O simples facto de se terem efectuado as medições várias vezes para cada pêndulo, tendo-se chegado a resultados semelhantes nos dois, torna praticamente nula a probabilidade de se cometerem erros como, por exemplo, medir repetidamente menos segundos do que o tempo real, ou medir mais de 10 cm a mais no comprimento do pêndulo. Isto partindo do princípio, naturalmente, que os aparelhos utilizados nas medições se encontrassem em condições normais de funcionamento, o que de facto acontecia.

Será, então, mais lógico procurar uma outra explicação para erros desta ordem. A mais óbvia é, naturalmente, uma falha do modelo utilizado ou, dito de outra forma, o facto dos pêndulos utilizados não serem ideais. Podíamos começar por considerar a hipótese de termos um amortecimento elevado, mas dois factos levam-nos a por essa hipótese de parte. Por um lado, observou-se, no decurso do trabalho laboratorial, muito pouco amortecimento no movimento dos pêndulos, mantendo-se a amplitude praticamente constante ao longo das vinte oscilações observados. Por outro, o amortecimento teria um efeito exactamente oposto aos erros observados. De facto, note-se que, como já referimos, no caso de o amortecimento do sistema não ser desprezável a frequência de oscilação será menor do que se o fosse. Ora, uma frequência menor significaria um período maior e no trabalho ocorreu exactamente o contrário, isto é, foram medidos períodos de oscilações menores do que os previstos teoricamente. Tal invalida um amortecimento não desprezável como explicação dos erros cometidos. A única hipótese alternativa facilmente encontrada é os pêndulos não serem na realidade simples mas sim compostos. Naturalmente que um pêndulo real nunca é simples, mas quando, neste contexto, dizemos que os pêndulos não eram simples estamos a afirmar que a massa da barra rígida que fazia ligação entre a massa e o apoio não era desprezável. Ora, em tal situação o comprimento do pêndulo utilizado na expressão não será o utilizado anteriormente mas sim um comprimento equivalente, dado pelo quociente entre o momento de inércia do pêndulo composto e o produto da massa do pêndulo pela distância do apoio ao centro de massa. Por não conhecermos exactamente qual a distribuição da massa no nosso pêndulo é-nos impossível o cálculo deste comprimento equivalente, mas é provável que se aproxime dos 73~74 cm calculados.

Temos, então, agora uma explicação plausível para as diferenças observadas e, assim, terminamos a nossa análise do mais simples de todos os movimentos oscilatórios, o movimento harmónico simples. Vamos, de seguida, recorrer ao conhecimento apresentado para estudarmos uma situação um pouco mais complexa, o caso de termos dois osciladores simples, como os observados, acoplados. Recorremos, para isso, aos resultados obtidos na primeira fase do trabalho, quer teóricos quer experimentais.

Ao contrário do que acontecia com o movimento harmónico simples, no qual o exemplo típico, o oscilador massa-mola, servia para analisar e deduzir o comportamento do sistema em estudo no trabalho laboratorial, no caso dos pêndulos acoplados um raciocínio semelhante já não será tão fácil. De facto, como veremos mais tarde, a montagem efectuada apresenta determinadas particularidades que não estão presentes no exemplo típico geral, que é o de termos um sistema constituído por dois osciladores massa-mola dos apresentados anteriormente, estando as massas desses dois sistemas ligadas por uma mola de acoplamento. Todavia, vamos, antes de nos debruçar sobre o sistema em estudo no trabalho laboratorial, vamos uma breve referência ao sistema constituído por dois osciladores acoplados.

No caso do nosso sistema propriamente dito, dos dois pêndulos ligados por um fio no centro do qual se encontra uma massa, a situação é já um pouco diferente. Este sistema pode ser modelizado pelo da figura, usando-se uma mola para representar o acoplamento. Note-se que, como o acoplamento está ligado não directamente à massa mas sim à barra rígida que o liga ao apoio, recorrermos não à relação mas sim à relação , isto é, a soma dos momentos das forças aplicadas é igual ao produto da aceleração angular pelo momento de inércia. Considerando a massa da haste do pêndulo desprezável, podemos aproximar o seu momento de inércia por ML², em que M é massa e L o comprimento. As equações, para ambos os pêndulos, ficam, neste caso:

Em que os índices de se referem ao pêndulo em questão. Resolvendo estas equações em ordem a temos que:

Se introduzirmos, para simplificar as expressões, as constantes:

      e      

e podem ser resolvidas recorrendo ao conceito da amplitude complexa. Temos, então, que:

Que tem soluções não triviais apenas se . Podemos, então ver, para cada uma das duas frequências possíveis, qual e expressão de e . Assim, para

Isto é, os dois pêndulos apresentam movimentos idênticos, à frequência que teriam caso não estivessem acoplados. Note-se que isto é lógico já que, se os pêndulos se movem exactamente da mesma forma, então e o acoplamento não tem qualquer efeito. Os pêndulos, já que, para todos os efeitos, são osciladores harmónicos livres, oscilam exactamente a frequência própria desse tipo de movimento.

Os dois pêndulos têm agora movimentos iguais mas em oposição de fase. Note-se que o acoplamento agora já tem efeito, conforme se pode ver na expressão da frequência angular do movimento; repare-se ainda que a posição do centro de massa não se altera mas os corpos movem-se em relação a este, ao contrário do movimento anterior, onde os corpos tinham sempre a mesma posição em relação ao centro de massa, mas a posição deste alterava-se ao longo do tempo, tinha um comportamento oscilatório.

No caso geral, o sistema terá um movimento que será a sobreposição destes dois modos de funcionamento, a que se dá o nome de modos normais. O primeiro modo de funcionamento, à frequência , é o modo simétrico, enquanto que o segundo, à frequência é o modo anti-simétrico.

Agora que já temos algumas noções sobre o funcionamento do sistema em estudo, vamos principiar a discussão do procedimento efectuado e, de seguida, a análise dos resultados obtidos. Quanto à montagem há pouco a dizer, sendo esta idêntica à utilizada na primeira fase do trabalho laboratorial, incluindo-se agora o acoplamento, constituído por um pequeno fio com uma massa presa no seu centro. O acoplamento foi montado a uma determinada distância da barra de apoio, tendo-se o cuidado de garantir que as suas ligações às barras rígidas dos pêndulos se encontravam numa posição o mais horizontal possível, isto é, à mesma distância da barra de apoio. Esta precaução foi tomada pois, como vimos anteriormente, o momento exercido sobre os pêndulos pelo acoplamento depende do ponto da haste onde é ligado e, assim, são necessárias distâncias iguais em ambos os pêndulos para que o efeito do acoplamento sobre eles seja também igual, como especificado no modelo em estudo. Foram encontradas algumas dificuldades, todavia, e este processo foi demorado, visto ter sido difícil, por razões de ordem técnica respeitantes ao material, estabelecer uma ligação segura do acoplamento a P2.

Tendo em conta que os efeitos do acoplamento dependiam da distância deste à barra de apoio, as várias medições efectuadas foram repetidas para três distâncias diferentes (nomeadamente 60, 35 e 15 cm) de modo a se poder analisar mais concretamente esta dependência. Apesar de, no trabalho laboratorial, se ter realizado todos os procedimentos para cada distância separadamente, isto é, terem sido realizadas todas as medições, inclusive as respeitantes ao fenómeno de batimento (que analisaremos mais tarde), para uma dada distância antes de se passar à seguinte, iremos, por uma questão de conveniência, tratar cada tópico (modos normais, batimentos,...) separadamente.  Por isto entenda-se que não nos dedicaremos primeiro aos resultados obtidos quando o acoplamento distanciava de 60 cm da barra de apoio, depois quando esta distância era 35 cm e finalmente 15 cm, mas sim analisaremos primeiro, para as três distâncias, os funcionamento do sistema nos modos normais, só nos debruçando sobre o fenómeno dos batimentos após esta análise estar concluída.

O primeiro objectivo no estudo dos pêndulos acoplados era, então, a determinação do período do movimento para ambos os modos normais. Assim, para o cálculo do período no primeiro modo, o modo simétrico, ambos os pêndulos foram movidos uma pequena distância (3 cm) no mesmo sentido e depois largados simultaneamente, medindo-se depois o tempo necessário para que completassem vinte oscilações. Note-se que aqui, novamente, se mediu o tempo de vinte oscilações e não apenas de uma, pelos mesmos motivos apresentados no caso do pêndulo simples. Quanto à distância que os pêndulos foram desviados da sua posição de equilíbrio, era necessário que esta fosse idêntica para ambos os pêndulos, de modo a termos, de facto, movimentos idênticos em cada pêndulo. Será fácil perceber, agora, a importância da precaução tomada na montagem original quanto à posição dos pêndulos na barra: o facto estes se encontrarem, no vertical, sobre pontos bem determinados da régua colocada na parte inferior da montagem em muito facilitou uma medição precisa do desvio horizontal de cada pêndulo. Quanto ao segundo modo, o modo anti-simétrico, o procedimento foi igual, tendo-se desviados os pêndulos horizontalmente de uma mesma distância de 3 cm, mas agora  em sentidos opostos. Note-se que, em ambos os passos, as medições foram realizadas para o pêndulo esquerdo (P1) tendo-se, contudo, o cuidado de verificar que o pêndulo direito (P2) possuía também o movimento desejado. Os resultados obtidos, nas várias repetições e para as várias distâncias do acoplamento à barra de apoio, encontram-se nas seguintes tabelas:

Distância do acoplamento à barra de apoio: 60 cm

Distância do acoplamento à barra de apoio: 35 cm

Distância do acoplamento à barra de apoio: 15 cm

Antes de procedermos a uma análise destes resultados façamos algumas observações. Note-se, antes de mais, que os valores finais obtidos foram todos arredondados até à centésima de segundo. É certo que utilizar uma maior precisão melhoria os resultados subsequentes. Contudo, recordemos que apenas podemos assegurar uma precisão de 0,025 segundos nos tempos medidos. Tendo isto em conta, até a precisão usada poderia ser considerada como exagerada, pelo que se optou por pelos arredondamentos utilizados. O ponto seguinte a notar diz respeito ao último conjunto de medições, para o caso em que a distância do acoplamento à barra de apoio é de apenas 15 cm. Nesta posição temos já um acoplamento muito fraco, e as medições efectuadas foram bastante mais difíceis. Os valores apresentados na última linha da tabela desta distância e respectivos valores associados deveriam, pela diferença para com os outros valores medidos, ser desprezados e, de facto, são, estando apresentados na tabela não tanto para o estudo dos modos normais mas sim para, mas tarde, estudarmos o fenómenos dos batimentos, onde veremos que com estes resultados o erro entre os tempos medidos e esperados será muito menor.

Comecemos, então, por analisar os dados respeitantes ao primeiro modo de funcionamento, o modo simétrico. Como esperado, estes valores são semelhantes aos obtidos no caso do pêndulo simples, notando-se apenas uma diferença mais significativa no primeiro caso. Ora, se recordarmos o comportamento do sistema nos modos normais isto é perfeitamente compreensível pois, no modo simétrico, ambos os osciladores movem-se de forma independente um do outro, têm movimentos sempre idênticos pelo que a distância entre eles não se altera e, assim, o acoplamento não tem qualquer efeito. A frequência de oscilação de ambos os pêndulos será, então, a frequência que estes teriam se apresentassem movimento harmónico simples, acontecendo,  naturalmente, o mesmo ao seu período. As diferenças observadas em relação ao resultado esperado (o obtido laboratorialmente, não o valor teórico esperado que já vimos não corresponder à realidade) são facilmente explicadas tendo em conta a grande variedade de factores no procedimento e na montagem com possibilidade de introduzir erro. O acoplamento podia não estar ligado às barras rígidas do pêndulo exactamente à mesma distância da barra de apoio, os pêndulos talvez não fossem exactamente iguais, os tempos medidos vêm afectados de ligeiros erros devido aos problemas de precisão referidos,... na realidade vários factores que, apesar de individualmente terem um efeito praticamente desprezável, poderiam afectar as medições significativamente em conjunto. O grande factor de erro, contudo, e aquele que consideraremos responsável pelas diferenças observadas, é a possibilidade de os pêndulos não estarem a oscilar de forma idêntica, isto é, o sistema não estar a funcionar no modo simétrico. Note-se que uma pequena diferença de tempo, um pequeno atraso na colocação dos dois pêndulos em movimento, ou mesmo uma pequena diferença nos desvios aplicados inicialmente (apesar das precauções tomadas), levaria a que o sistema funcionasse não no modo simétrico mas tivesse um movimento que fosse uma combinação linear dos dois modos normais. Esta suposição para a natureza do erro é suportada  pelo facto do maior erro observado, de 0,04 s, acontecer quando a distância do acoplamento à barra de apoio é maior (60 cm). Tendo em conta que o acoplamento tem um efeito tanto maior quanto maior for esta distância, é lógico que a maior diferença observada aconteça nesta situação.

Como conclusão da análise dos resultados obtidos para o modo simétrico vamos representar graficamente os valores do quadrado do período em ordem ao quadrado da distância à origem e realizar uma interpolação linear.

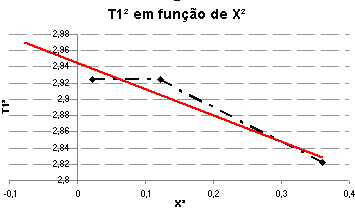Idealmente, o gráfico seria horizontal, já que o período de oscilação no modo simétrico é, em teoria, independente do acoplamento, sendo igual ao período quando os pêndulos têm movimento harmónico simples. Na realidade, por causa dos erros já referidos, tal não acontece, como podemos ver no gráfico. O declive da recta é de -0,39, valor que está de acordo com a análise apresentada anteriormente, pois é negativo, isto é, o período vai diminuindo com o aumento da distância do acoplamento à barra de apoio, e próximo de zero, que seria o declive obtido em situações ideais sem erro. A sua ordenada na origem é de 2,9572, valor cuja raiz é 1,72, exactamente o período obtido para o pêndulo esquerdo (P1) no estudo do movimento harmónico simples. Temos, então, a situação que pretendíamos: quando o sistema utilizado dos pêndulos acoplados funciona em modo simétrico, para todos os efeitos o acoplamento entre eles não existe. Isto é lógico visto que, se o movimento é exactamente igual para ambos os pêndulos, a distância entre estes permanece constante e, assim, o acoplamento, que pode ser modelizado por uma mola, não é comprimido nem distendido, não exercendo assim qualquer força sobre os pêndulos. Estes movem-se como se não existisse acoplamento, isto é, movem-se como pêndulos simples, apresentando assim período correspondente ao movimento harmónico simples e sendo aplicáveis as análises e resultados obtidos na primeira fase do trabalho laboratorial.

Tendo concluído a nosso estudo do primeiro dos dois modos normais de funcionamento, o modo simétrico, passemos agora à análise dos resultados obtidos para o funcionamento do sistema no segundo modo, o modo anti-simétrico, no qual ambos os pêndulos têm movimentos com a mesma frequência e amplitude, mas em oposição de fase. Comecemos por notar que, como agora a distância entre os pêndulos varia, o acoplamento já não tem um papel nulo no movimento, vai afectar o movimento dos pêndulos. É lógico, então, que os períodos do movimento medidos para este modo normal não sejam iguais (ou praticamente iguais) para as várias distâncias a que o acoplamento se encontrava da barra de apoio, como sucedia no caso do modo simétrico que estudamos anteriormente. De facto, recordemos a expressão para a frequência angular do movimento quando o sistema tem este tipo de movimento:

Em que L é o comprimento do pêndulo, M a sua massa, g a aceleração da gravidade, K a constante de acoplamento e x a distância do acoplamento à barra de apoio. Vemos aqui que a frequência angular do movimento aumenta com esta distância, o que está de acordo com os resultados obtidos. De facto, note-se que o período do movimento medido diminui com o aumento da distância, sendo de 1,70 s quando esta era de 15 cm, 1,62 s quando era 35 cm e, finalmente, 1,53 s quando o acoplamento distanciava 60 cm da barra de apoio. O período do movimento é inversamente proporcional à sua frequência angular, pelo que, quanto maior a distância do acoplamento à barra de apoio, maior a frequência angular, como previsto.

Note-se que, por não conhecermos os valores da massa do pêndulo e da constante de acoplamento, é-nos impossível calcular, para cada distância, os valores do período do movimento esperados teoricamente. Não será possível, então, compará-los com os valores obtidos no trabalho laboratorial, à semelhança do que foi feito para o estudo do primeiro modo normal. Assim, tomaremos a via contrária, isto é, tentaremos calcular o valor de 2K/M para o nosso sistema, partindo dos valores de x, g e L. Note-se que usaremos o valor de 9,8 ms^-2 para g e de 73,85 cm ( média dos dois comprimentos equivalentes encontrados anteriormente) para L. Temos, então, os seguintes resultados:

Curiosamente, estes valores, que deveriam ser iguais, parecem ter pouco em comum. Presumindo que o erro não está nem nas distâncias (x) nem no valor da aceleração da gravidade utilizado (que, apesar de poder variar, não se afastaria muito do valor utilizado), as hipóteses restantes são as frequências e os comprimentos equivalentes. Ora, as frequências foram calculadas directamente a partir dos períodos medidos e, apesar de todas as possibilidades de erro apresentadas para as medições até agora efectuadas poderem influenciar estes resultados, será muito mais sensato partir do princípio que estes tempos foram razoavelmente bem medidos, encontrando-se o grande problema no valor de L utilizado. De facto, note-se que se utilizou como L uma aproximação do comprimento equivalente do pêndulo, a média dos valores calculados para ambos os pêndulos quando se estudou o movimento harmónico simples. Então, não sendo L um valor obtido experimentalmente, resultante de medições efectuadas, mas simplesmente deduzido a partir destas, é provável que não corresponda à realidade e seja, deste modo, responsável pelas diferenças observadas. Como um pequeno exemplo vejamos como ficariam os valores de caso tivéssemos utilizado para L o valor calculado para o pêndulo esquerdo (o que até faz mais sentido, visto as medições terem sido realizadas para este pêndulo), de 73,4 cm.

Apesar de encontrarmos ainda um erro significativo para , note-se que os valores obtidos para as outras distâncias encontram-se muito mais próximos. Uma outra forma de procurarmos este valor seria termos em atenção que há uma relação do tipo entre e . De facto, temos que:

Se representarmos, num gráfico, os valores de em função de e realizarmos uma regressão linear chegamos aos seguintes valores:

E teríamos, se , e, então, . Quanto aos casos específicos de cada , teríamos agora:

Claramente, apesar de os valores serem bastante prometedores para as duas maiores distâncias do acoplamento à barra de apoio, o valor de para compromete as nossas expectativas. Poderíamos tentar procurar um valor de L que minimizasse as diferenças entre os valores de para as várias distâncias x, mas tal tarefa seria não só complicada mas talvez até um pouco fútil. De facto, os resultados obtidos são bastante sensíveis a variações de todos os parâmetros envolvidos e é possível que pequenos erros nestes estejam a contribuir significativamente para as diferenças obtidas. Note-se que, quando decidimos investigar os efeitos de L no valor da constante pretendida, partimos de determinados pressupostos que podem não se verificar. O valor da aceleração da gravidade poderia não ser e os erros nos períodos medidos laboratorialmente podiam não ser tão desprezáveis como pretendido. Conjugando todos estes factores, será difícil chegar a um valor de que satisfaça a todos os requisitos. Afinal, não conhecemos os verdadeiros valores de L, g e e, com as equações disponíveis, não possuímos meios de estimar o grau de confiança dos valores aproximados que temos, de calcular os valores esperados para cada parâmetro. Concluiremos aqui, então, a nossa análise do funcionamento do sistema dos pêndulos acoplados no modo anti-simétrico.

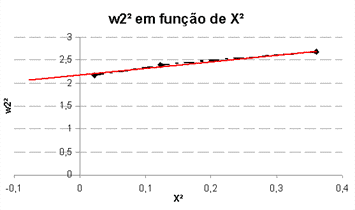Para concluir o estudo dos pêndulos acoplados vamos apresentar um novo tópico que foi objecto de estudo no trabalho laboratorial: o fenómeno dos batimentos. Este fenómeno surge quando temos dois movimentos oscilatórios de frequências semelhantes sobrepostos, resultando num movimento que pode ser visto como um movimento oscilatório com frequência igual a média das dos dois movimentos que o constituem, cuja amplitude é modulada de forma sinusoidal, a uma frequência dada pela diferença da dos dois movimentos originais. Para compreendermos melhor este fenómeno vamos ver o que acontece se, tendo o nosso sistema dos dois pêndulos acoplados, desviarmos apenas um deles uma pequena distância. Ora, sabemos já que, como estamos a tratar de osciladores acoplados o movimento será dado por uma combinação linear dos modos normais. Resolvendo para as condições iniciais dadas temos que:

Pelo que, as equações para e (respeitantes a P1 e P2) ficam:

Recorrendo às relações trigonométricas

Chegamos às expressões para e

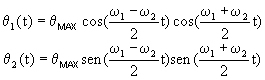
Temos, então, que e apresentam exactamente o movimento que descrevemos anteriormente, isto é, um movimento oscilatório, dado por

em que A, a amplitude, é

isto é, varia sinusoidalmente, também tem um comportamento oscilatório. Vejamos, de seguida, uma pequena representação deste movimento:

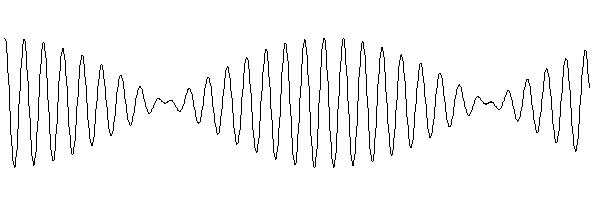Como podemos ver, o gráfico acima apresenta claramente uma sinusóide, representativa de um movimento oscilatório com frequência , a que se chama frequência de oscilação, , e cuja amplitude é modulada por uma outra sinusóide, de frequência inferior. Note-se que o valor da amplitude anula-se periodicamente, mais precisamente à frequência de , que é designada correntemente por frequência de batimento () visto serem exactamente estes anulamentos periódicos da amplitude que recebem o nome de “batimentos”. Se compararmos, para o nosso sistema, e , vemos que a única diferença entre um e outro é um desfasamento de 90º. O efeito é simples: a amplitude de um pêndulo atinge um máximo quando a do outro se anula. Experimentalmente, vemos um pêndulo a oscilar a uma dada frequência, com amplitude cada vez menor, à medida que a amplitude do movimento do outro pêndulo, que oscila à mesma frequência, vai aumentando até atingir um máximo no momento em que a amplitude do primeiro pêndulo se anula. O processo repete-se, tal como descrito, trocando agora os pêndulos de papel. É costume interpretar este movimento como uma transferência de energia entre os dois pêndulos: enquanto que um dado pêndulo está a oscilar, vai transferindo a sua energia ao outro que, consequentemente, oscila com uma amplitude cada vez maior. Assim que toda a energia do sistema se encontra neste segundo pêndulo e o primeiro, já sem energia mecânica, parou, o segundo começa a transferir a sua energia mecânica de volta ao primeiro pêndulo até que este possua toda a energia mecânica do sistema e todo o processo se reinicie.

Era necessário, então, medir os períodos de batimento do movimento e de oscilação. Sendo a situação idêntica para ambos os pêndulos, optou-se por se centrar as medidas no pêndulo esquerdo, estabelecendo-se assim uma continuidade com as outras fases do trabalho laboratorial, onde esta preferência também se verificou. Foi então P₁ que, à semelhança do explicado anteriormente, foi desviado ligeiramente (cerca de 3 cm na horizontal) e depois largado, estando P₂ inicialmente em repouso na sua posição de equilíbrio. A medição do período de batimento era teoricamente simples, bastando medir o tempo desde que se largasse P₁ até que o sistema estivesse nas mesmas condições que tinha inicialmente, isto é, P₁ com amplitude máxima e P₂ em repouso no seu ponto de equilíbrio. Contudo, foi necessário repetir várias vezes o procedimento pois era difícil identificar com precisão o momento exacto em que a amplitude do movimento de um pêndulo atingia o máximo e a do outro se anulava, particularmente se a distância do acoplamento à barra de apoio era pequena. A medição do tempo de oscilação provou ser ainda mais difícil, devido ao facto de amplitude variar continuamente, não sendo aqui possível medir o tempo necessário para se completarem várias oscilações e depois dividi-lo pelo número de oscilações. Deste modo, obteve-se o período através da medição do tempo necessário para que o pêndulo completasse apenas duas oscilações, dividindo-se depois este tempo por dois.

Os resultados finais obtidos (após se efectuarem as médias dos dados obtidos nas várias medições) estão apresentados na tabela acima. Antes de nos preocuparmos com os eventuais erros que estes resultados possam ter, vamos analisá-los numa perspectiva geral, verificando apenas se os resultados obtidos são, à partida, lógicos ou completamente absurdos. Note-se, então, que ambos os períodos medidos (de batimento e de oscilação) aumentam à medida que a distância do acoplamento à barra de apoio diminui. Ora, temos que, quanto menor esta distância mais a frequência angular do movimento no modo anti-simétrico se aproxima da frequência a que o sistema oscila no modo simétrico. De facto, recordemos as expressões para estas frequências, que confirmam o afirmado:

O que acontece, então, à frequência de oscilação e à de batimento ? Ora, já vimos que e . Assim, à medida que vai diminuindo com e se aproxima de , e diminuem também e aproximam-se, respectivamente, de e zero no limite. Uma diminuição progressiva de para valores muito pequenos leva a períodos de batimento cada vez maiores, enquanto que a diminuição de até leva a um aumento do período de oscilação até se atingir o período de oscilação do pêndulo simples (situação que, na realidade, só aconteceria quando , isto é, não teríamos acoplamento). É exactamente isto que acontece com os nossos valores: o período de batimento aumenta com a diminuição da distância do acoplamento à barra de apoio, atingindo valores razoavelmente grandes, enquanto que o período de oscilação se vai aproximando de 1,72 s, o período medido durante a primeira fase do trabalho laboratorial, atingindo para um valor já muito próximo. Os resultados obtidos são, então, lógicos, estando de acordo com o esperado.

Agora que já confirmamos que os valores medidos seguem o comportamento esperado, vamos analisá-los com mais detalhe de modo a verificar o quão próximos dos valores esperados teoricamente eles se encontram. Os valores esperados teoricamente podem ser calculados a partir das frequências obtidas anteriormente para o movimento do sistema dos pêndulos acoplados nos dois modos normais, e encontram-se na seguinte tabela:

Comparando os valores esperados teoricamente com os obtidos por medição directa vemos que, exceptuando o último caso do período de batimento, são razoavelmente parecidos. Naturalmente, praticamente todos eles apresentam um erro, erro esse que, em condições diferentes (como as da primeira fase do trabalho laboratorial, onde se estudaram osciladores simples), poderiam ser considerados elevados (cerca de 7% no período de batimento quando ). Todavia, dadas as dificuldades inerentes às medições destes tempos e também o facto que os valores esperados teoricamente foram, na realidade, calculados a partir de resultados com uma dada dose de erro, podemos considerar os resultados satisfatórios. Quanto ao caso do período de batimento medido quando a distância do acoplamento à barra de apoio era de 15 cm, é certo que aqui a diferença entre valor esperado e medido é extremamente grande, mas mesmo assim facilmente explicável. Como razões para tal temos, primeiro, a grande dificuldade de medir o período de batimento quando a distância do acoplamento à barra de apoio, e daí o efeito deste no sistema, é tão pequena, pois identificar correctamente os instantes pretendidos (duas anulações da amplitude seguidas no movimento de um dos pêndulos) é praticamente impossível; segundo, temos o facto de, exactamente pelo acoplamento ser fraco e ser muito próxima de , estarmos a lidar com subtracções de números muito parecidos, situação que é conhecida por conduzir a erros, dada a grande sensibilidade dos resultados à mínima alteração dos valores. Note-se, por exemplo, e daí a razão da apresentação dos resultados alternativos para , a enorme diferença (219,31 s) no cálculo do período de batimento que uma diferença de 0,03 s no período do movimento no modo anti-simétrico causa. Tendo estes factores em conta, facilmente se explica a enorme diferença entre o valor medido e o previsto para o período de batimento neste caso.

Por fim, de modo a rematarmos o estudo dos movimentos oscilatórios efectuado ao longo deste trabalho, voltaremos a um problema já abordado anteriormente, quando pretendemos calcular a constante no estudo do modo anti-simétrico: a determinação de g, a aceleração da gravidade, e L, o comprimento equivalente do pêndulo. Comecemos por notar que:

Pelo que podemos, a partir dos tempos medidos, calcular os valores de g e L. Supondo um valor de para o cálculo de L e de para o cálculo de g (o valor de L calculado para P1 quando , na primeira fase do trabalho laboratorial), obtemos os seguintes resultados:

Curiosamente, enquanto que no estudo do segundo modo normal, o modo anti-simétrico, os valores escolhidos para g e L conduziram a resultados de para as várias distâncias com diferenças significativas entre eles, os tempos medidos no estudo do fenómeno dos batimentos, que como já se referiu apresentam maior propensão para erros, levam a valores de g e L relativamente próximos entre si, com um erro relativo máximo de 4,1%. Note-se, aliás, que a média dos valores obtidos conduz exactamente à relação estabelecida entre g e L para P1 quando estudamos o movimento harmónico simples, isto é, o valor médio de g quando é de , enquanto que o valor médio de L quando é 73,43 cm. A propósito ainda destes valores, note-se que é justamente quando que os valores de g e L mais se aproximam dos pretendidos. Isto é lógico já que, nesta situação, o acoplamento entre os pêndulos é bastante fraco e, assim, o movimento do pêndulo esquerdo, relativamente ao qual foram feitas todas as medições, assemelha-se mais ao movimento harmónico simples, de onde foram retirados o par g e L utilizado. Note-se também que desta concordância com os valores esperados poderíamos concluir que os tempos medidos se aproximavam dos reais, devendo-se as diferenças entre estes e os calculados à custa de e não tanto a erros nas medições mas à grande sensibilidade dos cálculos com e .

Concluímos aqui, finalmente, o nosso estudo dos movimentos oscilatórios através da análise do comportamento de um sistema mecânico de pêndulos simples e pêndulos acoplado. Apesar de alguns problemas encontrados e ajustes feitos ao modelo proposto, nomeadamente o facto do pêndulo ser composto e não simples, tendo-se usado então o comprimento equivalente, pode-se afirmar que o modelo em estudo pode, de facto, ser aplicado ao nosso sistema, sendo possível chegar a resultados satisfatórios que permitam verificar experimentalmente vários aspectos inerentes ao modelo proposto, ao movimento em foco no trabalho prático laboratorial.